ECUACIÓN DE LA CIRCUNFERENCIA
Analíticamente
es una ecuación de segundo grado con dos variables, no toda ecuación de este
tipo representa siempre una circunferencia, solo en determinadas condiciones es
cierto. Una circunferencia queda completamente determinada si se conoce su
centro y su radio.
Algunos elementos de la circunferencia son:
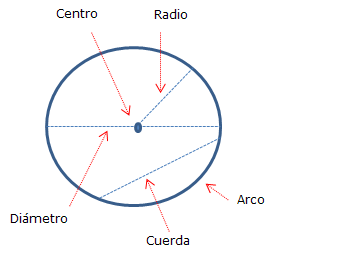
Centro: es el punto interior de la circunferencia que está a igual distancia de todos sus puntos.
Diámetro: es un segmento que une 2 puntos de la circunferencia pasando por su centro.
Radio: es un segmento que une cada punto de la circunferencia con el centro.
Cuerda: Es un segmento que une 2 puntos de la circunferencia sin pasar por el centro.
Arco: es el tramo de la circunferencia delimitado por una cuerda.
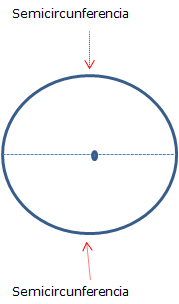
Semicircunferencia: Es la mitad de una circunferencia.
POSICIONES RELATIVAS DE UNA RECTA Y UNA CIRCUNFERENCIA
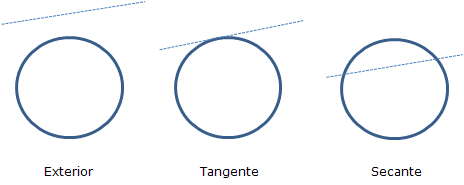
Exterior: la recta no toca ningún punto de la circunferencia
Tangente: la recta toca un punto de la circunferencia
Secante: la recta atraviesa la circunferencia y toca 2 puntos de la misma
POSICIÓN RELATIVA DE 2 CIRCUNFERENCIAS
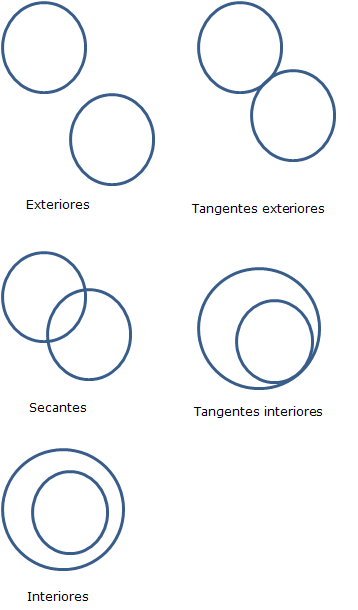
Exteriores: dos circunferencias que no se tocan en ninguno de sus puntos.
Tangentes exteriores: 2 circunferencias que se tocan en un punto.
Secantes: dos circunferencias que se cortan en 2 puntos.
Tangentes interiores: 2 circunferencias, una dentro de la otra, que se tocan en un punto.
Interiores: dos circunferencias, una dentro de la otra, que no se tocan en ninguno de sus puntos.
Ecuación Ordinaria de la Circunferencia
Dados las coordenadas del centro de la circunferencia C(h;k) y el radio "r" de la misma, podemos utilizar la siguiente ecuación para determinar el valor de "y" correspondiente a un valor de "x".
Ejemplo:
Hallar la ecuación de la circunferencia
cuyo centro es C(2;6) y con radio r = 4
(x - 2)² + (y - 6)² = 4²
Ecuación Canónica de la Circunferencia
Sean ahora las coordenadas del centro de la circunferencia C(0;0) y el radio "r", podemos utilizar la siguiente ecuación para determinar el valor de "y" correspondiente a un valor de "x".
Ejemplo:
Hallar la ecuación de la
circunferencia cuyo centro es el origen y con radio r = 3
x ² + y ² = 3²
Ecuación
General de la Circunferencia
Si conocemos el centro y el radio de una circunferencia, podemos
construir su ecuación ordinaria, y si operamos los cuadrados, obtenemos la forma
general de la ecuación de la circunferencia, así:
Ejemplo:
Hallar la ecuación
general de la circunferencia con centro C(2;6) y radio r = 4
(x - 2)² + (y - 6)² = 4²
x² - 2(2x) + 2² + y² - 2(6y) + 6² = 4²
x² - 4x + 4 + y² - 12y + 36 = 16
x² + y² - 4x - 12y + 4 + 36 - 16 =0
x² + y² - 4x - 12y + 24 = 0
D = -4 , E = -12 , F = 24
Observaciones:
Dada la ecuación de la
circunferencia x² + y² + Dx + Ey + F = 0 se cumple que:
Ejercicios
EJERCICIO 1
EJERCICIO 1
Encuentra la ecuación de la circunferencia centrada en el punto C(2, – 3) y radio 5. Grafica.
Todo punto que pertenezca a la circunferencia debe estar a distancia 5 del punto C(2, – 3), por lo
tanto debe verificarse que:
EJERCICIO 2
EJERCICIO 3
1 Hallar
la ecuación de la circunferencia inscrita en el triangulo cuyos lados son las
rectas.
L1= 2x - 3y + 21 = 0
L2= 3x - 2y - 6 = 0
L3= 2x – 3y + 9 = 0
EJERCICIO 4
Hallar la ecuación de la circunferencia que pasa por los puntos (2,3) y (3,6) y sea tangente a la recta 2x+y-2=0
Calculando la pendiente con los puntos (2,3) y (3,6) se obtiene:
Calculando la pendiente de la mediatriz que pasa pos los puntos (2,3) y (3,6) se obtiene:
Como la mediatriz es perpendicular al segmento formado al unir los puntos (2,3) y (3,6), por lo tanto la pendiente es la inversa negativa de 3, lo que da
Calculando el punto medio de (2,3) y (3,6) se obtiene:
Calculando la ecuación de la mediatriz al segmento formado por los puntos (2,3) y (3,6) se obtiene:
Realizando un gráfico se tiene:
Reemplazando los puntos (2,3) y (3,6) en la ecuación ordinaria de la circunferencia se obtiene:
Igualando las 2 ecuaciones anteriores de r2
Dividiendo por 2
Que es la ecuación de la mediatriz calculada anteriormente
Despejando h:
Calculando la distancia del radio de la circunferencia aplicando la ecuación de distancia de un punto C(h,k) a la recta 2x+y-2=0 se tiene:
Elevando al cuadrado la ecuación anterior:
Igualando la ecuación (6) con la (1)
Reemplazando la ecuación (3) en la anterior se tiene:
Resolviendo la ecuación obtenida:
Reemplazando los valores de k obtenidos en la ecuación (3) se halla los valores de h
Por lo tanto el centro C(h,k) de las circunferencias son:
Reemplazando los valores obtenidos en la ecuación (6) se calcula los radios:
Reemplazando los valores de h, k, y r en la ecuación ordinaria de la circunferencia se obtiene la solución al ejercicio
EJERCICIO 5
Determinar el ángulo formado por la intersección de la recta 
y la circunferencia 
Encontrando el centro y el radio de la circunferencia dada:
Calculando los puntos de intersección entre la recta y la circunferencia:
Graficando:
Calculando la pendiente del radio (El radio es perpendicular a la tangente de la circunferencia)
Calculando la pendiente de la tangente a la circunferencia por el punto (1,2)
Calculando la ecuación de la tangente a la circunferencia por el punto (1,2)
Calculando la pendiente de la recta 
Calculando el ángulo 
de intersección entre la recta y la circunferencia
EJERCICIO 6
Hallar la ecuación de la circunferencia que pasa por el punto (-2,2) y por los puntos de intersección de las circunferencias x2+y2+3x-2y-4=0 y x2+y2-2x-y-6=0.
Aplicando la ecuación de la circunferencia
Reemplazando el valor encontrado se tiene:
Graficando se obtiene:
y la circunferencia de intersección entre la recta y la circunferenciaVIDEOS DE EJERCICIOS RESUELTOS DE LA CIRCUNFERENCIA
EJERCICIOS PROPUESTOS
Ejercicios:
Hallar las ecuaciones de las siguientes circunferencias:
1. Centro (0, 0) y radio 3.
2. Centro (2, -3) y radio 5.
3. x2 + y2 = 4.
4. El centro es e1 punto de intersección de las rectas: 2x + 5y -2 = 0, x -2y + 8 = 0,
y pasa por el punto (2, -1).
5. Tiene su centro en la recta 2x -y -10 = 0 y pasa por los puntos (1, 3) y (5, -3).
6. Pasa por los puntos (1, 3) (4, 0) y (1, -1).
7. Pasa por el origen y por los puntos (- 2, 0) y (3, 3).
8. Pasa por los puntos (11, 1) (3, -3) y es tangente a la recta 3x + 4y + 13 =0.
